Introduction
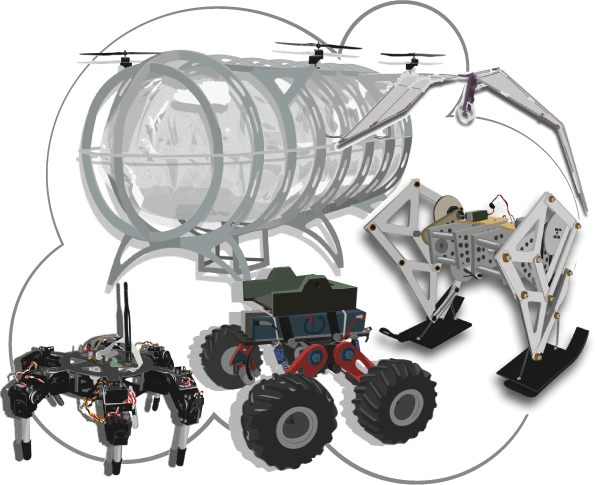
The Robotics Laboratory conducts both fundamental and practical research in the realm of computational mobile robotics. Our research endeavors encompass various aspects, including the design of robotic structures, the modeling of physical systems, simulation techniques, and the applied control of a diverse range of robotic systems—ranging from actuated and under-actuated to bionic robotics. A significant focus of our group lies in exploring mechanical design, conducting mathematical analyses, and developing numerical models for physical robotic systems. Our research spans four distinct modalities: rolling, walking, swimming, and flying robots. This multifaceted approach allows us to delve deeply into the intricacies of each modality, contributing to a comprehensive understanding and advancement of robotic technologies. About Us The Robotics Laboratory, led by the Mechatronics research group and established in August 2007 by Dr. Edgar A. Martínez-García, is dedicated to fostering theoretical analysis, applied mathematical methodologies, computational simulation in robotics, and the practical implementation of experimental projects. Our research approach is centered on cultivating individual student projects, employing this as a shared strategy to facilitate effective skill development. Within the laboratory, we equip students with the tools for engaging in multidisciplinary engineering activities, empowering them to hone both theoretical understanding and practical skills in the field of robotics. Our research is focused on the development of innovative models for autonomous robots, and our specific pursuits within this domain include:
- Simulating and mathematically modeling physical robotic systems.
- Applying dynamic control to mobile robotic functions, including navigation, planning, and sensing.
- Design, analysis and modeling of under-actuated robotic mechanisms.
- Analyzing and modeling bionic robots, including biomechanical models and their motion.
- Researching deterministic sensor fusion models through physics-based integro-differential equations.
- The application of scientific computing and mathematical methods for modeling robots.